 레이더, LIDAR, 적외선 및 투시 카메라, 기타 방식들을 포함한 자동차 센서 시스템이 계속해서 복잡성과 성능이 높아지고 있다. 이 글에서는 Altera의 Cyclone V SoC FPGA를 이용해서 자동차 레이더 시스템의 디지털 프로세싱 부분을 구현하는 것에 대해서 소개한다. 맞춤형 ASIC과 비교해서 이 기법의 장점은 제품 출시 시간 단축, 현장 업그레이드, 그리고 사전에 통합된 부동소수점 듀얼 ARM Cortex-A9 마이크로프로세서 시스템을 이용해서 빠르고 편리하게 구현할 수 있다는 것이다.
레이더, LIDAR, 적외선 및 투시 카메라, 기타 방식들을 포함한 자동차 센서 시스템이 계속해서 복잡성과 성능이 높아지고 있다. 이 글에서는 Altera의 Cyclone V SoC FPGA를 이용해서 자동차 레이더 시스템의 디지털 프로세싱 부분을 구현하는 것에 대해서 소개한다. 맞춤형 ASIC과 비교해서 이 기법의 장점은 제품 출시 시간 단축, 현장 업그레이드, 그리고 사전에 통합된 부동소수점 듀얼 ARM Cortex-A9 마이크로프로세서 시스템을 이용해서 빠르고 편리하게 구현할 수 있다는 것이다.
레이더는 군사적 목적과 상업용으로 오래 전부터 사용돼 왔다. 최근에는 고가 자동차에서 주차지원이나 차선이탈경고에 레이더 기술이 사용되고 있다. 차세대 차량 레이더 시스템은 주행 중 충돌방지 및 적응형 순항제어장치(Adaptive Cruise Control, ACC) 등에서 아주 중요한 역할을 하므로 매우 정교해야 한다. 단순히 경고 신호를 제공하는 것이 아니라 주행 중인 자동차를 제어하는 시스템에 레이더를 적용하기 위해서는 시스템 신뢰성 요구가 훨씬 더 엄격해지며 자동차 충돌에 대한 책임 가능성 또한 발생할 수 있다.
이 글은 디지털 신호 처리(DSP) 디자인을 설계하기 위한 신속한 프로토타이핑 및 개발 툴 플로로서 Altera의 DSP Builder Advanced를 이용해서 어떻게 자동차 레이더 시스템의 디지털 프로세싱 부분을 빠르고 편리하게 구현할 수 있는지 설명한다.
이 결과는 레이더 프로세싱의 디지털 부분의 실제 회로 크기와 성능을 가늠해 볼 수 있는 예를 제시한다. 이 디지털 프로세싱은 낮은 가격대의 FPGA 패브릭으로 강력한 듀얼 600 MHz ARM Cortex-A9 프로세서를 통합한 SoC FPGA라고 하는 새로운 유형의 프로그래머블 로직을 이용하고 있다. SoC FPGA는 레이더, LIDAR, 적외선 및 투시 카메라 등의 애플리케이션에 이용할 수 있도록 유연성과 확장성이 뛰어난 플랫폼을 제공한다. 뿐만 아니라 FPGA 하드웨어와 ARM 소프트웨어 구현 둘 다 부동소수점 프로세싱을 이용함으로써 FPGA나 ASIC을 이용한 기존의 고정소수점 구현과 비교해 레이더 애플리케이션으로 훨씬 더 뛰어난 성능을 제공한다.
SoC FPGA 기법은 생산 라인 상에서 또는 현장에서 소프트웨어 및 하드웨어 펌웨어 업데이트가 가능하다.
이 점은 자동차 레이더 시스템이 계속해서 복잡도가 높아지고 있기 때문에 매우 중요하다. 또한 SoC FPGA는 카메라를 이용한 비디오 프로세싱을 통합하기에 적합하다. 레이더 검출 정보와 함께 비디오 분석 프로세싱을 결합함으로써 “센서 융합”을 달성할 수 있다. “센서 융합”은 다중의 센싱 시스템을 결합해서 의사결정의 토대로 이용할 수 있도록 가장 신뢰할 만한 데이터를 제공한다. 센서 융합은 미래의 첨단 운전자지원 시스템(ADAS)에서 점점 더 중요한 역할을 할 것으로 기대된다.
자동차 레이더에 이용하기 위한 펄스 도플러 기법
많은 레이더 시스템이 펄스 도플러(pulse-doppler) 기법을 채택하고 있다. 펄스 도플러 기법은 트랜스미터가 짧은 간격 동안 동작하고 다음 송신 펄스 때까지 수신 모드가 되는 것이다. 펄스 도플러 레이더는 펄스 반복 간격(Pulse Repetition Interval, PRI)이라고 하는 특정한 간격으로 연속적인 펄스를 전송한다. 레이더는 되돌아오는 반사파를 코히어런트하게(coherently) 처리해서 검출된 물체의 거리와 상대적 움직임을 추출할 수 있다. STAP (Space Time Adaptive Processing) 같은 좀 더 정교한 프로세싱 기법은 레이더 반사를 추가적으로 처리함으로써 해당 물체 주변의 지면 반사 산란(ground clutter)이나 백그라운드 리턴 등에 의해서 심하게 방해를 받는 경우라도 목표 데이터를 추출할 수 있다.
자동차 레이더는 도달 거리가 짧게는 수 미터에서 길게는 수백 미터에 이를 수 있다. 2 m 거리일 경우에 레이더 펄스의 왕복 송신 시간은 13 ns이다. 이와 같은 짧은 거리는 트랜스미터와 리시버가 동시에 동작해야 하므로 각각 안테나가 필요하다. 펄스 도플러 레이더는 주기적으로 펄스를 전송하며, 총 경과 시간에 대해서 트랜스미터가 작동하는 시간 비율이 듀티 사이클이다. 듀티 사이클이 통상적으로 낮으므로 이 비율에 따라서 총 송신 전력이 제한된다. 이 전력은 다시 검출 거리를 제한한다. 1~2 m 거리 분해능을 달성하기 위해서는 또한 100 MSPS 이상의 샘플 레이트를 필요로 하며 거리와 도플러 차원 모두에서 데이터를 디지털적으로 처리할 수 있어야 한다. 이러한 높은 샘플 레이트가 레이더 시스템의 비용을 상승시킬 수 있다.

또 다른 기법으로 연속 파장 주파수 변조(Continuous Wave Frequency Modulated, CWFM)라는 레이더 기법을 이용할 수 있다. CWFM은 펄스를 전송하고 반사 또는 레이더 에코를 모니터하는 방식 대신에 반송파 주파수를 연속적으로 송신하는 방식이다. 연속적 반사 에코로부터 유용한 정보를 추출하기 위해서 그림 1에서 보는 것과 같이 반송파 주파수를 시간의 경과에 따라서 지속적으로 높였다가 낮춘다. 트랜스미터와 리시버 모두 연속적으로 동작한다. 이 글에서 설명하는 시스템의 경우는 송신 신호가 리시버로 유입되는 것을 방지하기 위해서 분리된 송신 및 수신 안테나를 이용한다.
레이더는 검출된 물체의 거리를 계산할 수 있어야 한다. CWFM 기법은 송신 주파수와 수신 주파수의 순간적인 차이(델타)를 측정해서 거리를 계산한다. 송신 사이클의 양의 주파수 경사 구간일 때는 수신 주파수가 시간 지연만큼 송신 주파수보다 일정하게 낮을 것이다. 송신 사이클의 음의 주파수 경사 구간일 때는 수신 주파수가 역시 시간 지연만큼 송신 주파수보다 높을 것이다. 이러한 주파수 차이, 다시 말해서 오프셋은 왕복 지연 시간에 비례할 것이므로 거리를 측정할 수 있는 수단을 제공한다. 거리가 길수록 트랜스미터에서 리시버로 시간 지연이 높아질 것이다. 송신 주파수가 연속적으로 변화하므로 특정한 순간에 송신 주파수와 수신 주파수 사이의 차이가 송신 신호가 레이더에서 목표물로 이동했다가 되돌아오는 데 걸리는 시간에 비례할 것이다.
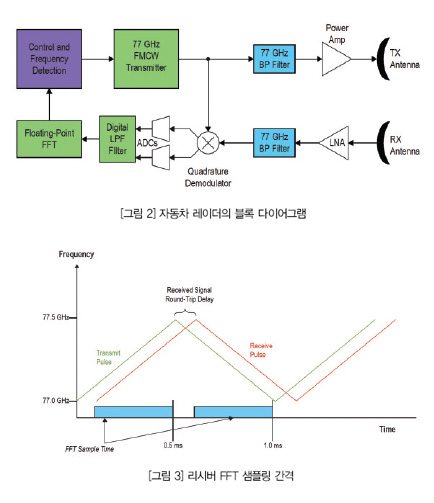
그림 2는 CWFM 레이더의 블록 다이어그램 예이다. 자동차 레이더는 밀리미터 대로 동작하므로 송신 신호의 파장은 수 밀리미터 대이다. 통상적으로 이용되는 주파수는 24 GHz(λ = 12.5 mm) 및 77 GHz(λ = 3.9 mm)이다. 이 주파수를 주로 이용하는 것은 필요한 안테나 크기가 작고, 스펙트럼을 이용하기가 상대적으로 편리하고, 무선 신호를 빠르게 감쇠할 수 있기 때문이다(자동차 레이더의 거리는 수백 미터로 제한적이다). CWFM 기법을 이용하면 진폭 변조가 일어나지 않으며 트랜스미터만 주파수를 변화시킨다. FM 기법을 이용하면 송신 회로가 RF 증폭기로 가장 효율적인 모드로서 포화 모드로 동작할 수 있다.
아날로그 믹서 회로를 이용함으로써, 수신 저역통과 필터(LPF)가 수신 신호와 송신 신호의 차이만 통과시키면 되고 송신 사이클 시에 수신 신호의 500 MHz 대역폭을 통과시키지 않아도 된다. 이와 같이 신호들의 차이를 통과시키는 것에 대해서 예를 들어 설명하는 것이 이해하기 쉬울 것이다. 예를 들어 시스템의 거리 양 극단인 1 m 거리와 300 m 거리로 반사를 수신한다고 하자.
주파수 경사가 0.5 ms에 500 MHz이면, 다시 말해 ns에 1 kHz이면 수신 신호의 주파수는 3 × 108 m/s의 빛의 속도를 이용했을 때 다음과 같다:
1 m 거리 = 2 m 왕복 지연 = 2 m
÷ (3 × 108 m/s) = 7 ns
300 m 거리 = 600 m 왕복 지연
= 600 m ÷ (3 × 108 m/s) = 2 μs
양의 주파수 경사 구간일 때 1 m 거리의 물체의 반사는 -kHz 오프셋이 될 것이다. 음의 주파수 경사 구간일 때 1 m 거리의 물체로부터의 반사는 +7 kHz 오프셋이 될 것이다.
양의 주파수 경사 구간일 때 300 m 거리의 물체의 반사는 -2 MHz 오프셋이 될 것이다. 음의 주파수 경사 구간일 때 300 m 거리의 물체의 반사는 +2 MHz 오프셋이 될 것이다.
이러한 오프셋으로서 반사를 일으키는 물체의 거리에 따라서 리시버가 ±2 MHz 대의 주파수를 경험하게 될 것이라는 것을 알 수 있다. 이 주파수는 그림 3에서 보는 것과 같은 시간 간격으로 FFT(Fast Fourier Transform)을 적용해서 검출할 수 있다. 리시버가 5 MSPS로 샘플링하면 리시버 FFT 샘플링 간격이 약 0.4 ms 일 때 2,048 포인트 FFT를 이용할 수 있다. 그러면 주파수 분해능이 1 kHz이므로 1 m의 수 분의 일의 거리 분해능을 달성하기에 충분하다. FFT 출력의 보간을 실시함으로써 분해능을 향상시킬 수 있다. 이렇게 구한 주파수 오프셋은 리시버 거리 반사는 제공할 수 있으나 이를 이용해서 마주 오는 자동차, 같은 방향으로 주행하는 자동차, 비슷한 거리의 정지된 물체 등을 구분하지는 못한다. 이러한 구분이 가능하기 위해서는 반사에 대해서 도플러 주파수 편이(doppler frequency shift)를 이용해야 한다.
이 또한 예를 들어 설명하는 것이 도플러 주파수 편이를 어떻게 검출할 수 있는지 이해하기 가장 쉬울 것이다. 예를 들어 77 GHz 레이더를 장착한 자동차가 시속 80 km 속도로 주행하고 있고(그러므로 초당 22.2 m) 30 m 거리에 3개의 물체가 있다고 하자. 하나는 시속 50 km 속도로 마주 오는 자동차이고, 다른 하나는 같은 방향으로 시속 100 km로 주행하는 자동차이고, 또 다른 하나는 정지된 물체라고 하자. 물체가 거리를 좁혀져올 때는 도플러 주파수 편이가 양이므로, 다시 말해 반사 신호가 송신 신호보다 주파수가 높을 것이다. 직관적으로 알 수 있듯이, 이 동작은 거리가 좁혀짐에 따라서 신호의 파고가 서로 가까워지는 것으로 보이기 때문이다. 반대로 레이더와 목표물 사이의 거리가 벌어지면, 다시 말해 거리가 멀어지면 음의 도플러 주파수 편이가 될 것이다. 도플러 편이의 양은 공식 1에서와 같이 계산할 수 있다.
공식 1: 도플러 편이(Doppler Shift)
도플러 주파수 편이 = (2 × 속도 차이) ÷ 파장
50 km/h의 속도로 마주 오는 자동차/ 80 km/h로 주행하는 레이더를 장착한 자동차/ 130 km/h 또는 36.1 m/s의 접근 속도
도플러 주파수 편이 =
2 (36.1 m/s) ÷ (.0039 m) = 18.5 kHz
정지된 물체, 80 km/h로 주행하는 레이더를 장착한 자동차, 80 km/h 또는 22.2 m/s의 접근 속도
도플러 주파수 편이 =
2 (22.2 m/s) ÷ (.0039 m) = 11.4 kHz
100 km/h의 속도로 앞서가는 자동차, 80 km/h로 주행하는 레이더를 장착한 자동차, 20 km/h 또는 5.56 m/s의 멀어지는 속도(opening rate)
도플러 주파수 편이 = -2 (5.56 m/s)
÷ (.0039 m) = -2.8 kHz
이러한 도플러 편이는 양의 주파수 경사 및 음의 주파수 경사 구간에서 검출된 주파수 차이를 오프셋 시킨다. 상대적인 움직임이 없고, 그러므로 도플러 편이가 없다면 수신 주파수의 차이가 동일할 것이다. 다만 양의 주파수 경사와 음의 주파수 경사 시에 부호가 반대가 될 것이다. 그러므로 송신 신호의 양의 주파수 경사 구간과 음의 주파수 경사 구간의 수신 주파수 오프셋을 비교함으로써 도플러 편이를 구할 수 있다. 공식 2에서는 이 관계를 설명하고 있다. 이 공식을 적용해서 FFT 출력이 트랜스미터의 양의 주파수 경사 및 음의 주파수 경사 시의 결과들을 이용해서 거리와 상대 속도(relative velocity)를 계산할 수 있다.
공식 2: 상대 속도(Relative Velocity)
상대 속도(target to radar) = (wavelength ÷ 2) × (positive ramp detected frequency - negative ramp detected frequency) ÷ 2

그림 4는 리시버가 경험하는 주파수와 FFT에 의해서 처리되는 주파수를 보여준다. 리시버는 국부 발진기(LO)로 송신 신호와 일정한 위상 관계에 있는 국부 발진 신호를 수신 신호에 가해서 복조, 다시 말해서 다운컨버팅하므로 FFT가 송신 파형과 수신 파형 사이의 주파수 차이를 처리한다. 그림 4에서는 한 목표물의 펄스 반사만을 보여주고 있으나 각기 다른 목표물(이 예의 경우 3개 목표물)이 다중의 주파수를 발생시키는 것을 FFT로 검출할 수 있다.
다시 위에서 든 예를 살펴보면, 30 m 거리에 3개의 목표물이 있다. 시속 50 km의 속도로 마주 오는 자동차, 같은 방향으로 시속 100 km로 주행하는 또 다른 자동차, 정지된 물체가 그것이다. 레이더를 탑재한 자동차는 시속 80 km로 주행하고 있다(22.2 m/s). 30 m 거리의 3개 목표물 모두 리시버 주파수 오프셋은 다음과 같다.
30 m 거리 = 60 m 왕복 지연
= 60 m ÷ (3×108 m/s) = 200 ns
주파수 오프셋은 음의 주파수 경사 및 양의 주파수 경사 각각이 ±200 kHz이다.
거리 지연으로 인한 주파수 오프셋에 도플러 오프셋을 더해야 한다. 표 1은 이들 값을 요약해서 보여주고 있다.
이렇게 계산된 음의 및 양의 주파수 오프셋만을 이용해서 공식 3, 4, 5를 적용해서 목표물의 거리 및 상대 도플러 편이를 계산할 수 있다. 레이더 장착 자동차의 순방향 속도가 알려져 있으므로 목표물의 속도를 쉽게 계산할 수 있다. 마찬가지로 레이더의 주파수 경사율(ramp rate) 역시 알려진 수치이다.

공식 3: 거리(Range)
거리 = (빛의 속도 ÷ (4 × 주파수 경사율)) ×
(음의 주파수 오프셋 - 양의 주파수 오프셋)
공식 4: 상대 속도(Relative Velocity)
상대 속도 = (빛의 속도 ÷ (4 × 반송파 주파수)) × (음의 주파수 오프셋 + 양의 주파수 오프셋)
공식 5: 절대 목표물 속도(Absolute Target Velocity)
절대 목표물 속도 = 상대 속도 - 레이더 장착차량 속도
이 예의 경우에 주파수 경사율은 0.5 ms에 500 MHz이므로 초당 1,000 GHz 비율이다. 위의 값들을 대입해보면 다음을 구할 수 있다.
50 km/h 속도로 접근해오는 자동차:
거리 = (3·108 ÷ (4 × 1000 × 109)) ·
(218.5 × 103 - -181.5 × 103) = 30 m
상대 속도 = (3·108 ÷ (4 × 77 × 109)) ×
(218.5 × 103 + -181.5 × 103) =
36m/s = 130 km/hr
절대 목표물 속도 =
130 - 80 = 50 km/hour closing rate
나머지 목표물들도 같은 방식으로 계산할 수 있다.
여러 목표물이 존재할 때 고려해야 할 중요한 문제는 양의 경사 구간 및 음의 경사 구간의 주파수들을 어떻게 쌍을 지어야 할지 확실하지 않을 수 있다는 것이다. 이와 같은 문제를 레이더 용어로 모호성(ambiguity)이라고 한다. 이 문제를 해결하기 위해서 특수한 기법을 필요로 하며 펄스 도플러 레이더에서보다는 CWFM 레이더에서 좀 더 복잡한 문제가 된다.
이 문제에 대한 한 가지 방법은 경사 지속시간 및 주파수에 변화를 주고 검출된 주파수가 각기 다른 주파수 경사에 따라서 스펙트럼 상에서 어떻게 이동하는지를 검사하는 것이다. 이와 같이 변화를 줌으로써 각 목표물의 음의 주파수와 양의 주파수를 정확하게 짝 지을 수 있다. 경사를 대략 ms에 한 번 변화를 줄 수 있으므로 1초의 간격에 수백 개의 이러한 변화를 분석할 수 있다. 주파수 경사와 지속시간 설정을 제어하고 음의 주파수 및 양의 주파수 경사 시에 검출된 FFT 출력 주파수를 이용해서 목표물의 거리와 도플러를 계산하는 것은 통상적으로 제어 프로세서가 하는 일인데, 이 제어 프로세서를 SoC FPGA의 ARM Cortex-A9 프로세서 중의 하나로 구현할 수 있다.
여타의 센싱 기법을 함께 이용할 수 있다. 카메라를 이용하면 자동차로부터의 강한 반사와 사람으로부터의 약한 반사를 구분할 수 있다. 스테레오 카메라를 이용하면 영상 분석 기법을 이용해서 거리를 계산하는 것이 가능하다.
또 다른 가능한 방법은 멀티모드 레이더로서 탁 트인 고속도로에서는 CWFM을 이용해서 좀 더 긴 거리에서 목표물을 검출하고, 좀 더 짧은 거리에서 더 많은 목표물 반사가 이뤄지는 도심 지역에서는 짧은 거리의 펄스 도플러 레이더를 이용할 수 있다. 펄스 도플러 레이더는 혼잡한 목표물 환경에서 모호성 검출 문제가 좀 덜하다.
레이더 링크 예산
레이더 성능은 링크 예산 공식에 의해서 제한된다. 이 공식은 어떠한 수준의 수신 신호를 검출에 이용할 수 있을지를 결정한다. 공식 6은 단순화된 레이더 링크 예산 공식을 보여주고 있다.
공식 6: 레이더 링크 예산(Radar Link Budget)
Prcv = Ptrx × G2 × σ × λ2 × τ ÷ ((4π)3 × R4)
여기서,
Ptrx는 링크 송신 전력이다.
G는 송신 및 수신 안테나 이득이다.
σ는 목표물의 레이더 단면도 다시 말해 면적이다.
λ는 레이더 파장이다.
τ는 트랜스미터의 듀티 사이클이다.
R은 목표물의 거리이다.
흔히, 데시벨(dB)이나 dBm(1 mW를 기준으로 한 dB)을 이용해서 로그 스케일로 파라미터들을 표시한다. 이 예에서는 이 스케일을 이용하고 있으며 와트 단위 수치 또한 표시하고 있다. 다음 부분의 설명에서는 다음과 같이 가정한다. 달성 가능한 리시버 잡음 지수가 5 dB 일 때 리시버 감도는 약 -120 dBm(10-15 W)이 될 것이다. 타당한 주파수 검출을 달성하기 위해서 20 dB의 신호대잡음비(SNR)가 요구된다고 한다면, Prcv가 최악 상황일 때 최소한 100 dBm(10-13 W)이어야 한다.
안테나 이득은 30 dB, 다시 말해서 1000을 이용한다. 파라볼릭 안테나의 경우에는 공식 7과 같이 안테나 boresight 방향의 이득을 계산할 수 있다.
공식 7: 안테나 boresight 이득
G = 4πAeff ÷ λ
그러면 77 GHz로 동작하는 안테나에 필요한 면적은 0.0012 m2라는 것을 구할 수 있는데, 그렇다면 직경이 0.04 m, 다시 말해서 4 cm로서 자동차 전면에 탑재하기에 매우 적정한 크기라고 할 수 있다.(다만 유의할 점은 최소한 한 개의 송신 안테나와 한 개의 리시버 안테나 필요하다는 것이다.)
CWFM의 듀티 사이클 τ는 100%, 다시 말해서 1이다. 송신 전력이 0.1 W(20 dBm)이고, 최대 거리가 300 m이고, 목표 자동차 반사 면적이 1 m2라고 한다면 적정한 조건들일 때 최악상황 수신 전력을 다음과 같이 구할 수 있다.
Prcv = (0.1 × 1,0002 × 1 × .00392 × 1) ÷ ((4π)3 × 3004) = 9.4 × 10-14 W or -100 dBm
2 m의 아주 가까운 거리이고 단면적이 10 m2라고 했을 때(견인 트레일러의 후면), 적정한 조건들일 때 예상할 수 있는 최대 Prcv를 다음과 같이 구할 수 있다.
Prcv = (0.1 × 1,0002 × 1 × .00392 × 10) ÷ ((4π)3 × 24) = 4.8 × 10-4 W or -3.2 dBm
이러한 계산으로서 이 글에서 설명하고 있는 시스템 예는 120 dB 대의 매우 높은 동적 범위를 제공하는 리시버를 필요로 한다는 것을 알 수 있다. 높은 동적 범위는 리시버와 아날로그-디지털 컨버터(ADC)에 대해서 매우 높은 선형성을 요구한다. 그런데 불과 2 m 거리의 대형 목표물은 다른 목표물을 검출하기 위한 레이더의 LOS(line-of-sight)를 방해할 수 있다. 그러므로 아날로그 자동 이득 제어(AGC) 루프를 이용해서 극단적인 대형의 반사가 존재할 때 리시버의 감도를 낮춤으로서 리시버와 ADC의 동적 범위를 낮출 수 있다.
4 m 거리의 1 m2 목표물 같이 좀 더 덜 까다로운 목표물을 검출하면서 이보다 먼 거리의 다른 목표물들 또한 검출하고자 할 때는 최대 감도가 바람직할 수 있다. 이 경우에 이 대형 반사는 다음과 같이 수신 전력을 구할 수 있다:
Prcv = (0.1 × 1,0002 × 1 × .00392 × 1) ÷ ((4π)3 × 44) = 3.0 × 10-6 W or -25 dBm
AGC를 이용함으로써 동적 범위 요구를 약 95 dBm으로 낮출 수 있으므로 16비트 ADC를 이용해서 달성할 수 있다. 일정한 마진을 확보하기 위해서는 ADC를 (나이퀴스트 기준 이상으로) 32× 오버샘플링으로 동작시킴으로써 추가적인 유효 3비트를 달성하거나 아니면 양자화 잡음 플로어를 추가적으로 18 dB 낮출 수 있다. 또 다른 방법으로서 18비트 ADC를 이용할 수 있으나 이 방법은 훨씬 더 가격이 비쌀 것이다.
구현 고려사항
CWFM 레이더 아키텍처의 이점은 아날로그 및 디지털 구현 모두 간소하다는 것이다. 아날로그 측에서 트랜스미터는 직접 디지털 합성기(Direct Digital Synthesizer, DDS)와 표준적인 레퍼런스 수정발진기를 이용해서 구현할 수 있다. DDS가 아날로그 주파수 경사 레퍼런스를 발생시킴으로써 PLL(Phased-Locked Loop)이 원하는 송신 주파수 변조를 발생시키도록 한다. 예를 들어 PLL이 분주기(divider)가 1000이라고 한다면, 이 글 예의 경우에 5 MHz 주파수 경사일 때 레퍼런스는 중심이 77 MHz가 될 것이다. 이 아날로그 경사 신호가 PLL의 레퍼런스를 구동함으로써 77 GHz 발진기를 제어한다. 이 회로의 발진기 출력이 증폭되고 77 GHz의 중심 주파수로 500 MHz 비율로 상승하고 하강하는 연속 파장(CW) 신호를 발생시킨다. 77 GHz에서의 필터링 및 매칭 회로들은 high-epsilon R 유전체 회로 카드로 에칭된 수동소자들을 이용해서 구현함으로써 필요한 부품 수를 최소화할 수 있다. 그림 5는 아날로그 회로의 블록 다이어그램을 보여준다.

리시버는 프론트엔드에 필터링 및 저잡음 증폭기(LNA)와 이어서 쿼드러처 복조기를 필요로 한다. 쿼드러처 복조기는 77 GHz 수신 신호와 경사 송신 신호를 믹싱해서 특정한 시점에서의 송신 파형과 수신 파형 사이의 차이를 포함하는 복합적인 기저대 신호를 발생시킨다. 목표물 반사의 거리와 도플러 편이에 따라서 고정적인 주파수인 것에서 알 수 있듯이 경사는 제거된다. 여기서도 또한 에칭 수동소자들을 이용해서 77 GHz의 고주파 필터링을 구현할 수 있다. 쿼드러처 복조기의 출력은 최대 거리일 때 최대 ±2 MHz로서 저주파이다. 그러므로 전통적인 수동소자와 연산증폭기를 이용해서 in-phase(I) 및 쿼드러처(Q) ADC에 앞서 에일리어싱 방지 저역통과 필터링을 구현할 수 있다. 또 다른 방법으로 IF(Inter mediate Frequency) 아키텍처를 이용할 수 있는데, 그러기 위해서는 오프셋 수신 LO 생성 회로를 필요로 한다.
I 및 Q 입력을 제공하는 ADC는 나이퀴스트 기준을 충족하기 위해서 최소 5 MSPS로 동작해야 한다. 그런데 만약에 40 MSPS의 8× 샘플링 주파수를 이용하고 이어서 8:1 디지털 데시메이션(decimation) 필터를 이용하면 약 3비트의 추가적인 분해능을 달성할 수 있다. 이와 같은 데시메이션을 이용함으로써 16비트 ADC가 실제적으로 18비트~19비트 대로 동작할 수 있으므로 100 dB을 훨씬 넘는 동적 범위를 달성할 수 있다.
디지털 필터는 16비트 I 및 Q 입력 샘플을 이용해서 160 MHz 레이트로 동작하고 5 MHz로 샘플을 출력할 수 있는데 24비트로 반올림된다. 신호처리의 다음 단계는 FFT를 이용해서 주파수 판별을 실시하고, 이어서 보간 회로를 적용하는 것이다. FFT의 특성은 프로세싱 스테이지를 거듭할수록 데이터 정밀도가 높아지는 것이다. 이 글 예의 경우에는 2,048 포인트 FFT인 것으로 가정하는데, 그러면 어떠한 데이터 소실을 방지하기 위해서 최대 10개의 추가적인 비트의 정밀도를 요구할 수 있다. 그런데 FFT를 단정밀도(Single precision) 부동소수점 프로세싱으로 구현하면 이와 같은 비트 증가를 피할 수 있다. FFT로 최대치의 24비트 가수(mantissa) 정밀도(23비트 + 부호)를 유지할 수 있으며 100 dB 이상의 동적 범위를 편리하게 지원할 수 있다. 그러므로 가까운 거리의 강한 반사 때문에 먼 거리의 약한 목표물 반사가 장애를 받지 않으며, 그러므로 레이더 시스템이 가까운 거리의 강한 반사 때문에 “blinded” 되지 않는다. 부동소수점 프로세싱은 또한 약한 반사가 FFT의 디지털 잡음 플로어로 “buried”되지 않도록 한다. 그림 6은 디지털 회로의 블록 다이어그램을 보여준다.
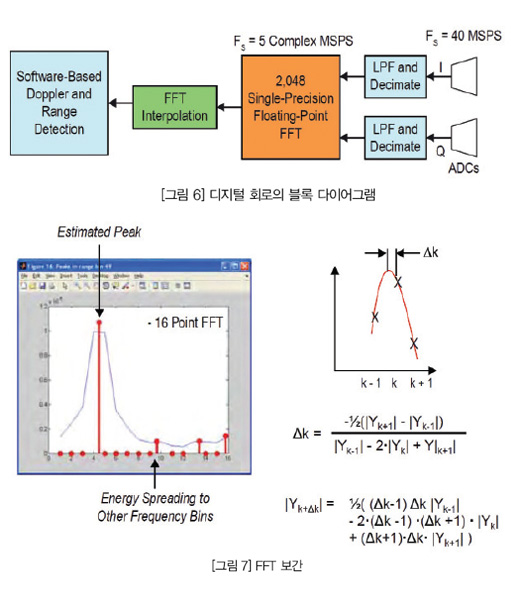
부동소수점 FFT 회로는 또한 160 MHz로 클로킹 할 수 있다. 다만 복잡한 데이터는 10 MSPS로 프로세싱 한다. 부동소수점 회로는 Altera의 DSP Builder Advanced 툴 플로우를 이용함으로써 훨씬 더 적은 로직을 이용해서 구현할 수 있다. 또한 완전 부동소수점 회로를 구현함으로써 클록 레이트가 데이터 레이트보다 높을 때 데이터패스를 “folding” 할 수 있으므로 로직과 DSP 블록 자원을 절약할 수 있으며, 그러므로 전력 소모를 줄일 수 있다. Cyclone V SoC FPGA로 DSP Builder 툴을 이용해서 타이밍 클로저(timing closure) 프로세스를 자동화함으로써 이러한 최적화를 달성할 수 있다. Cyclone V SoC FPGA는 18×19 및 27×27 곱셈기 크기를 지원하는 DSP 블록을 제공한다. 대형의 27×27 곱셈기 크기는 부동소수점 디자인에 이용하기에 적합하다.
FFT 출력을 보간함으로써 정밀한 주파수 판별이 가능하다. 만약 신호의 에너지가 주파수 빈(frequency bins) 이내이면 그림 7에서와 같이 보간 기능이 FFT 에너지를 다른 빈으로 에일리어싱함으로써 약한 목표물이 소실되지 않도록 한다.
검출 프로세싱은 온칩 ARM Cortex-A9 마이크로프로세서 중의 하나를 이용해서 할 수 있다. 간단한 임계값에서부터 좀 더 정교한 CFAR (Constant False Alarm Rate)에 이르는 알고리즘들을 이용할 수 있다. FFT 결과의 보간은 시스템 디자이너의 선택에 따라서 로직으로 구현하거나 소프트웨어로 구현할 수 있다.
간섭 고려사항
시스템 디자이너들은 다수의 자동차가 결국 77 GHz로 동작하는 레이더를 장착하게 될 것임을 고려해야 한다. 그러면 마주 오는 자동차의 레이더 트랜스미터가 대다수 목표물 반사보다 훨씬 강한 신호를 발생시킬 것이다. 그런데 트랜스미터는 이 예의 경우에는 500 MHz로서 수백 MHz 이상으로 동작한다. 리시버 입력 대역폭은 5 MHz 대로서 송신 대역폭의 약 1%이다. 간섭은 마주 오는 자동차의 트랜스미터가 자신의 대역폭의 이 1%를 스윕(sweep) 할 때 동시에 다른 리시버 역시 이 특정한 대역폭을 스윕 할 때만 일어난다. 통계적으로 이러한 중복은 그렇게 빈번하게 일어날 가능성이 낮으며, 만약 그렇게 되었을 때는 송신 경사 타이밍을 임의적으로 조절함으로써 그러한 중복을 제거할 수 있다. 이러한 문제는 다수의 장비들이 공유 채널을 통해 랜덤 액세스 기법을 이용해서 간헐적으로 통신하는 시스템에서 흔하게 발생하는 문제이다.
빔성형(beamforming) 기술
지금까지 설명한 레이더 시스템은 자동차 바로 앞의 목표물을 제외하고는 안테나 빔폭(beamwidth) 내에서 목표물의 거리와 속도는 검출할 수 있으나 목표물의 방향에 대해서는 정보를 제공하지 못한다. 시스템이 레이더 송신 또는 수신 안테나 방향성을 스윕 또는 스티어(steer) 할 수 있으면 스윕된 목표물 반사 에코의 변화를 모니터함으로써 방향을 판단할 수 있다. 이 글에서 설명하는 시스템은 파라볼릭 안테나를 이용하는 것으로 가정한다. 파라볼릭 안테나는 송신 또는 수신 전자기파를 특정한 방향으로 집중시킨다. 집중시키는 정도는 안테나 면적과 파장에 따라서 결정된다. 밀리미터 파장 레이더를 이용함으로써 소형 안테나를 이용할 수 있다.
파라볼릭 안테나는 기계적으로 원하는 방향을 향하도록 “조준”이 가능하다. 이 성능은 기계적 운동 속도와 신뢰성 및 비용적 요인에 의해서 제한된다. 이에 대해, 널리 이용되는 대안적 기법이 전자 빔 스티어링 기법을 이용하는 것이다. 이 기법은 안테나가 개별적인 수신 또는 송신 안테나로 이루어진 선형 또는 방형 어레이가 되도록 하는 것이다. 개별 안테나 신호들을 코히어런트하게 결합할 수 있으므로 보강 및 상쇄 파면(wave front)을 결합함으로써 특정한 방향으로는 이득을 극대화하고 다른 방향으로는 이득을 최소화할 수 있다.
자동차 레이더의 경우는 레이더를 상하로 스티어링 할 필요가 없으므로 2차원 안테나 어레이가 필요하지 않다. 선형 어레이, 다시 말해서 안테나 라인을 이용해서 안테나를 애지머스 스티어링(side by side) 할 수 있다. 단점은 비용과 복잡성이다. 이 예의 경우에는 수신 신호의 디지털 프로세싱으로 인해 수신 방향 스티어링은 좀 더 간단하다. 각각의 리시버가 개별적으로 수신 신호 위상을 조절해야 한다.
이와 같은 위상 조절이 안테나 빔의 방향을 스티어링 할 수 있도록 한다. 수신 신호가 모든 안테나 요소에 걸쳐서 동위상으로 도착할 때라야 최대의 신호 강도가 발생한다. 어레이 안테나는 안테나의 메인 로브(main lobe)를 원하는 방향으로 “조준”할 수 있다. 각각의 안테나 요소들이 지연 또는 위상 조절이 이루어져서 이 조절 후에는 모든 안테나 요소들이 공통의 신호 위상이 되도록 한다. 각도 θ = 0이면 모든 안테나 요소가 동시에 신호를 수신하고 위상 조절이 필요하지 않다. 0이 아닌 각도일 때는 그림 8에서 보는 것처럼 각각의 안테나 요소가 지연을 조정해서 안테나 어레이 전체에 걸쳐서 파면을 정렬하도록 한다.

전자식 스티어링 안테나는 N개 안테나 수신 노드 각각에 대해서 아날로그 리시버 회로를 복제해야 한다. 다행히 밀리미터 레이더는 안테나 패치, 필터, 매칭 회로 등의 다수의 회로를 직접적으로 PCB 상에서 구현할 수 있다. LNA, 쿼드러처 복조기, ADC 역시 N개 노드 각각에 대해서 복제해야 하며, ADC가 비용적으로 영향을 미치는 요인이 될 수 있다.
디지털적으로, 각 안테나 노드의 ADC 쌍으로부터 제공되는 I 및 Q 입력의 각 세트는 위상을 지연시켜야 한다. 이 지연은 복소수 곱셈기를 이용해서 N개 수신 노드 각각에 대해서 N개의 각각의 복소수 계수 Wi를 이용해서 이뤄진다. Cyclone V SoC FPGA의 DSP 블록은 이 기능에 이용하기에 적합하도록 설계됐으며, 한 개의 DSP 블록이 높은 속도로 전체적인 복소수 곱셈기를 구현할 수 있다. 제어 프로세서가 N개 복소수 계수를 주기적으로 업데이트해서 수신 안테나를 “스윕”하고 목표물 반사 진폭의 변화를 모니터한다. N 크기 4에서부터 16에 이르는 빔성형 기법을 지원하기 위해서 아주 소량의 추가적인 FPGA DSP 블록 및 로직 자원을 필요로 한다.
전방 주시 자동차 레이더의 경우에는 원하는 애지머스 스티어링(azimuth steering) 각도가 자동차 중심선으로부터 5~10도 정도뿐이다. 비용 상의 경제성을 위해서 안테나 로브 빔 폭이 충분한 파라볼릭 송신 안테나를 이용하고 좀 더 좁은 폭의 로브 빔 스티어링 수신 안테나를 이용해서 각기 다른 애지머스로 목표물을 구분할 수 있을 것이다. 또 다른 방법으로는 좀 더 복잡한 트랜스미터 및 송신 빔성형 안테나를 이용해서 원하는 송신 애지머스 방향으로 더 높은 이득을 달성할 수 있는데, 이 방법은 비용과 복잡성을 증가시킨다.
멀티모드 레이더 시스템
짧은 거리일 때는 펄스 도플러 레이더가 적합할 수 있다. 펄스 도플러 레이더는 검출 거리가 짧아야 한다. 짧은 듀티 사이클을 이용하므로 송신 전력이 CWFM의 수 분의 일에 불과하기 때문이다. 펄스 도플러 레이더는 검출 모호성을 최소화할 수 있다는 것이 장점이며, 단점은 더 높은 샘플 레이트 및 신호 프로세싱 레이트를 필요로 하고 외부적인 메모리 스토리지를 사용해야 한다는 것이다. 예를 들어 100 MHz(10 ns)의 샘플 레이트와 64개 거리 빈(bins)을 이용하면 약 100 m 왕복 거리가 가능하며 거리 분해능은 약 1.5 m이다. 64개 송신 펄스로부터의 응답을 수집함으로써 각 거리로 64개 샘플을 이용해서 도플러 검출이 가능하다. 필요한 스토리지는 64 × 64 = 4096 복소수 샘플로서 이를 프로세싱 할 수 있도록 저장해야 하므로 외부적인 DDR 메모리 칩을 필요로 한다. Altera SoC FPGA는 하드 구현 DDR 메모리 컨트롤러를 포함한다. 메모리 대역폭은 이 DDR을 DDR 컨트롤러 중재를 통해서 ARM 프로세싱 서브시스템과 공유할 수 있을 정도이다.

거리 및 도플러 판별을 이용해서 그림 9에서 보는 것처럼 이 두 차원으로 목표물을 분해할 수 있다. 250 kHz의 펄스 반복 비율을 이용하면 펄스 간격이 4 μs이므로 거리 문제를 없앤다. 한 펄스로부터의 목표물 반사가 다음 PRI에 나타나기 위해서는 거리가 1,200 m 이상의 왕복 거리, 다시 말해 600 m 거리여야 하며 결과적인 감쇠로 인해서 이러한 반사는 검출되지 못할 것이다. 또한 250 kHz의 확장된 PRI를 이용하면 도플러 모호성이 문제가 되지 않을 것이다(레이더가 각각의 수신 간격을 샘플링하고 다음 송신 펄스 전까지 잠시 멈춘다). 부동소수점 프로세싱을 이용함으로써 거리(“fast” 시간)와 도플러(“slow” 시간)로 플롯을 구할 수 있으며 소프트웨어로 검출 프로세싱을 실시할 수 있다.
SoC FPGA를 이용할 때의 장점은 부분적 재구성가능성을 이용해서 수 밀리 초 이내에 CWFM에서 펄스 도플러 레이더로 동작 모드를 전환할 수 있다는 것이다. 그러므로 FPGA는 이 두 모드를 동시에 지원할 필요가 없으므로 하드웨어 자원을 절약할 수 있다. 또한 부분적 재구성가능성을 이용할 때 ARM 프로세싱 서브시스템이나 인터페이스 회로 같은 FPGA의 다른 부분들이 계속해서 동작할 수 있으며 부분적 재구성가능 프로세스의 영향을 받지 않는다.
FPGA 자원 활용 예측
표 2와 표 3은 Altera의 Quartus Ⅱ 소프트웨어를 이용해서 얻어진 FPGA 자원 예측이다. CWFM 디자인이 펄스 도플러 디자인보다 훨씬 더 적은 자원을 활용한다는 것을 알 수 있으며, Altera의 낮은 가격대의 SoC FPGA를 이용해서 CWFM을 편리하게 구현할 수 있다.
AEM(오토모티브일렉트로닉스매거진)
<저작권자 © AEM. 무단전재 및 재배포 금지>